DOE - Design Of Experiment

• Design Of Experiment - Experimententwurf

Die DOE Technik, die die Erkenntnisse des japanischen Fachmanns Dr. Taguchi nutzt, ist ein sehr effektives Mittel für die Verbesserung der Produktqualität und zur Kostenreduzierung. Die geeignetsten Bereiche für den Einsatz dieser Technik sind gerade Forschung und Entwicklung, weiterhin das Testen und die Validierung. In neuester Zeit ist diese Technik sehr verbreitet, z.B. auch von führenden Fahrzeugherstellern, wie Ford, GM und VW.

DOE ermöglicht die Lösung von komplizierten und komplexen Aufgaben, wenn das Endergebnis von einer Vielzahl von Faktoren beeinflusst wird. Deshalb ist es notwendig, umfangreiche Analysen mit einem Hilfsmittel durchzuführen, welches in der Lage ist, die gesamte Analyse zu umfassen. Das Ziel ist die Feststellung der kritischen Faktoren, deren Optimierung sowie die Minimierung der Variabilität, um am Schluss ein robustes Modell vorliegen zu haben, in dem die Charakteristiken gegenüber der Wirkung der natürlichen Umwelteinflüsse sich als möglichst widerstandsfähig erweisen. Es handelt sich nicht nur um rein statistische Methoden, sondern auch um die Verflechtung der analytischen mit den statistischen Techniken.

Vom Standpunkt der Vorentwicklungsetappen aus, können mit Hilfe der DOE Technik die konstruktiven und herstellungstechnischen Alternativen einer Lösung untersucht werden, unter Berücksichtigung der gegenseitigen Interaktion und Beeinflussung. Das Hauptanliegen ist die Vorhersage des Systemverhaltens in der Zukunft und die Entdeckung seiner Verbesserung. In dieser Phase können wir durch die DOE Applikation qualitativen Problemen bei der Endproduktion vorbeugen und somit die Kosten senken. Die Methodik kann selbstverständlich in jeder Phase der Planung und Vorbereitung der Produktentwicklung, des Prozesses und der eigenen Serienproduktion eingesetzt werden.

Die Methodik DOE gehört zu den Mitteln, die eine wirklich präzise Vorbereitung vor der eigentlichen Experimentrealisierung erfordert. Als Erstes ist es notwendig, die Aufgabe zu analysieren, die genaue Eingabe festzulegen und den Grundeintritt für die eigene Planung der Experimente vorzubereiten. Die Zeit für die Vorbereitung wird aber leicht zurückgewonnen, weil Dank der Vorbereitung nur wirklich unbedingt erforderliche Experimente durchgeführt werden.

CFD - Computational Fluid Dynamic

• Computational - Nutzung der Mathematik mit Computertechnik
• Fluid Dynamics - der Teilchen, die dem Gegenüber in Bewegung sind

CFD ist eine Berechnungstechnologie, die die Beobachtung der Dynamik strömender Teilchen ermöglicht. Bei CFD Verwendung ist es möglich, virtuelle Berechnungsmodelle zu bilden, die allgemeine Systeme oder Anlagen repräsentieren und Dank derer das Verhalten von Flüssigkeiten mit allen seinen Gesetzmäßigkeiten wie Wirbel, Grenzschichten und ähnlich vorhergesagt werden kann. CFD Programme bieten den Effektor für die Simulierung der Strömung von Flüssigkeiten und Gasen, der Wärme- oder Masseübertragung, der Interaktion zwischen festem und luftigem Teil der Aufgabe und mechanischer Schwingungen. Bei Verwendung der CFD Analyse können wir den virtuellen Prototyp des Systems oder Prozesses darstellen, der später im Zeitablauf nachfolgen kann und anschließend die Reaktion des Verhaltens gegenüber verschiedenen Impulse analysieren. Die verwendeten CFD Programme bietet dem Benutzer eine große Menge an Ausgaben in Form von Daten oder graphischer Darstellungen, mit denen man einfach das Verhalten der modellierten Baugruppe feststellen kann.

FEM - Finite Element Method

• Finite Element Method - Methode der Finiten Elemente

Die Methode der Finiten Elemente ist eine numerische Methode, die zur Simulation des Spannungsverlaufs, von Deformationen, eigenen Frequenzen, Wärmeströmungen, Elektromagnetismus usw. an einem dargestellten physikalischen Modell dient. Das Prinzip liegt in der Diskretisierung des stetigen Kontinuums in einer bestimmten (endgültige) Anzahl der Elemente, wobei die festgestellten Parameter in einzelnen Knotenpunkten bestimmt sind. FEM wird verwendet vor allem für die Kontrolle schon entworfener Anlagen, oder für die Festlegung der kritischen (am meistens beanspruchten) Stellen der Konstruktion. Obwohl die Prinzipien der Methode schon lange Zeit bekannt sind, ist es zur Massenanwendung erst Dank der Entwicklung der modernen Computertechnik gekommen.

Allgemeiner Vorgang der Simulationen CFD/FEM

Der Vorgang der gesamten Modellierung ist immer in mindestens drei Phasen verteilt. Die erste umfasst Preprocessing Aufgaben, d.i. Modellvorbereitung (Vorbereitung der Geometrie und des Berechnungsnetzes des Modells, Definition des physikalischen und materiellen Modells, Bestimmung der Randbedingungen usw.), die zweite eigene Berechnungen (Solver) und die letzte dann Postprocessing, d.i. die Darstellung, Auswertung und Interpretation der Ergebnisse.

Preprocesing

Es handelt sich um den ersten Schritt bei der Anfertigung des neuen Berechnungsmodells und beinhaltet die Erstellung oder Abänderung des geometrischen Modells unter Anwendung von CAD (Computer-Aided Design) Programmen, sowie die Erstellung und Kontrolle des oberflächlichen und volumetrischen Berechnungsnetzes und den Export in Berechnungssoftware.

Die an häufigsten benutzten Programme können schon gefertigte CAD-Geometrien einlesen. Anwendung finden weiterhin Mittel, die es ermöglichen, nicht wichtige Details des Modells, die unnötig die Ansprüche an die Computertechnik erhöhen und für die eigene Analyse unerheblich sind, zu vereinfachen. Zur gefertigten Modellgeometrie wird am Ende ein oberflächliches und volumetrisches Netz (mesh) appliziert, welches die konkreten Forderungen der numerischen Simulation berücksichtigt.

Berechnung (Solver)

CFD Programme führen aufgrund des Berechnungsnetzes und der eingestellten Randbedingungen die geforderten Berechnungen durch und speichern die Ergebnisse in Dateien, die zur weiteren Bearbeitung dienen.

• Mehrphasige Strömung
• Reaktion der Materialien
• Verschiebung und Deformation von Gehäusen durch Druckbelastung
• Turbulenzmodelle
• Radiation, Konvektion, Konduktion
• Akustik, Verbreitung mechanischer Schwingungen

Postprocesing

Es handelt sich um den Abschlussschritt von kompletten Analysen, bei dem anhand der berechneten Werte, Bilder oder Animationen deren Interpretation durchgeführt wird. Die richtige Interpretation der einzelnen Ergebnisse ist sehr wichtig und erfordert einen erfahrenen Fachmann, der in der Lage ist, aufgrund eigener Erfahrungen und Fachkenntnissen deren konkrete Analyse durchzuführen.

Zum Postprocessing ist es allgemein möglich, sowohl die Mittel des eigenen Berechnungsprogrammes, als auch spezialisierte Software zu nutzen, die meist eine viel breitere Auswahl an Möglichkeiten bietet.

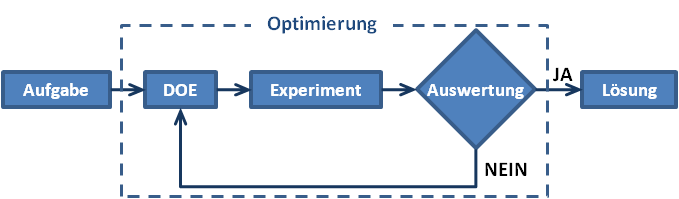
Optimierung

Es handelt sich um die Suche nach den bestmöglichen Lösungsmöglichkeiten aufgrund geeigneter Zielfunktionen in einem Bereich mit bestimmten Beschränkungen.

Grundlage für jede Optimierung ist ein parametrisches Modell, das durch schnelle Parameteränderung das Modell eines bestimmten Teils zu modifizieren ermöglicht. Zuerst ist es notwendig, die Zielfunktion zu definieren und die beschränkenden Bedingungen festzulegen. Für die automatische Führung des Optimierungsprozesses steht heute eine Vielzahl von kommerziellen Systemen zur Disposition. Diese Programme beinhalten gewöhnlich eine große Menge von Optimierungsalgorithmen, das sind klassisch gradiente, genetische Methoden, DOE, deren Kombinationen, Annäherungsfunktionen und eine ganze Reihe von weiteren Mitteln. Allgemein versuchen die Optimierungsmethoden extrem (min/max) definierte Zielfunktionen zu finden und das durch die Abänderung der gegebenen Parameter bei Einhaltung der beschränkenden Bedingungen. Im Falle der 3D Formoptimierungen ist es günstig die Methoden anzuwenden, die die niedrigste Anzahl an Berechnungszyklen erfordern.

• RSM/DOE (Response Surface Method)
• Gradiente Methoden
• Evolutionäre Methoden
• NN (Neural Network)

• MACK (Multivariate Adaptive Crossvalidating Kriging)
• FBM (Falling Ball Method)

Gegenwärtig setzt sich immer mehr auch unterschiedlicher Zugang durch, der die Einhaltung der Topologie des ursprünglichen Netzes ermöglicht und die Formenänderung des bestimmten Bereiches direkt durch Knotenverschiebung der einzelnen Elemente durchführt, sgn. Morphing des Berechnungsnetzes. Anbieter dieser Technologie sind zum Beispiel SCULPTOR und ANSA.